The Mandelbrot Set and Everything Else

Pick a number. Square it. Now square that new number. Repeat. Continue indefinitely. If you picked a number greater than 1, your number continued to get bigger and bigger:

2² = 4 —> 4² = 16 —> 16² = 256 …

If you picked a number between 0 and 1, your number got smaller and smaller:

.5² = .25 —> .25² = .0625 —> .0625² = .0039 …

And yet again, a number less than -1 would yield endlessly larger numbers:

-2² = 4 —> 4² = 16 —> 16² = 256 …

Depending on the number first selected, iterations of squaring that number will result differently.

Now, let’s start with the number 0. Obviously, squaring 0 forever does nothing for us. So, let’s also add a number (C), then send this new number back through the system:

0² + C

Let’s see what happens when C is equal to 1.

For C = 1:

0² + 1 = 1 → 1² + 1 = 2 → 2² + 1 = 5 → 5² + 1 = 26…

The number simply continues to get larger.

Let’s see what happens when C = -1:

For C = -1:

0² - 1 = -1 → -1² - 1 = 0 → 0² - 1 = -1 → -1² - 1 = 0…

-1 behaves differently. It will continue to produce this endless back and forth. So, while iterations of 1 bring us to infinity, iterations of -1 keep us bound.

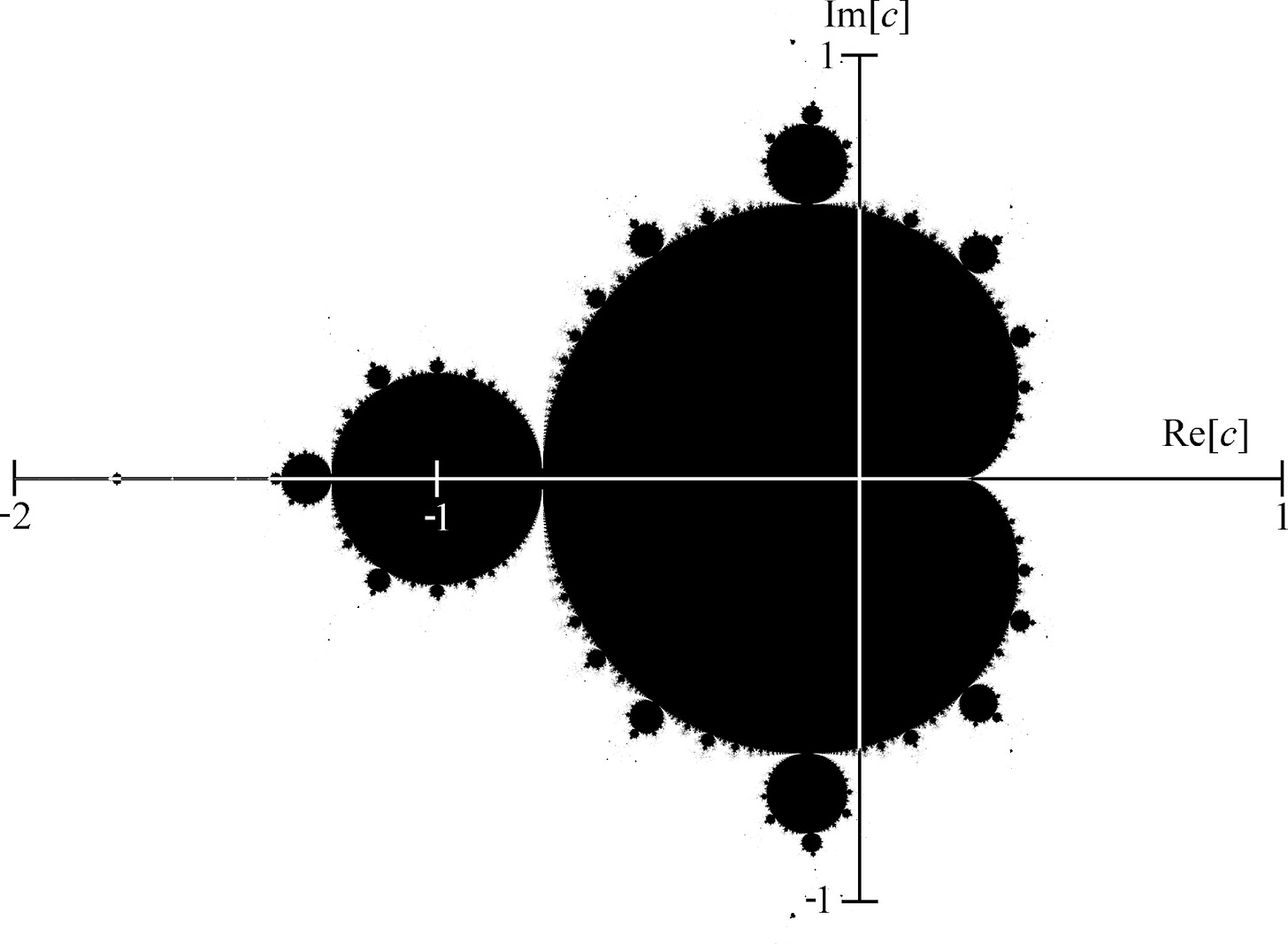
What we’ve just considered is what’s at the heart of one of the most famous objects in all of mathematics: the Mandelbrot Set. The Mandelbrot Set is a set of numbers that happen to stay bounded under iterations of the equation we’ve just considered (0² + C)* . As such, -1 is indeed in the Mandelbrot Set, as iterations stay bounded, while 1 is not inside the Mandelbrot Set because it “blows up” to infinity, when iterated.

*The actual mathematical expression for the equation that gets iterated to create the Mandelbrot Set is formally written as Z_n+1 = Z_n² + C where Z₀ = 0 and C is a complex number.

But the Mandelbrot Set isn’t just considering numbers on the real number line. It’s considering numbers along something called the complex plane, which consists of these things called complex numbers. This so-called complex plane charts real (Re) numbers along the x-axis and imaginary (Im) (i defined as the square root of -1) along the y-axis.

Example of a complex number within the Complex Plane, credit: https://mathematica.stackexchange.com/questions/200070/plotting-complex-numbers-as-arrows-on-the-complex-plane

When you plot the numbers of this plane that stay bounded under such iterations, you get the famous beetle-like shape named after Benoit Mandelbrot, its discoverer.

Without the axis, in color.:

In combining the reals with the imaginary numbers, we can produce something very complex simply by iterating a rather basic equation. The complexity of the Mandelbrot Set lies at its border. Zooming in on its border famously reveals an infinite pattern of self similarity. Shapes repeat in similar ways forever. The Mandelbrot Set is a shape that contains a finite area, yet has an infinite border.

This complexity along the border is analogous to the complexity of real life binary options, conditions, definitions or choices we encounter as humans. The Mandelbrot Set, in a sense, asks a binary question: is a given number inside or outside the set? Yet the border of where one becomes the other is infinite. There is no border, as such. The closer one gets to the border, the less certain one is to know which side of the border one resides on. Similarly, when it comes to concepts, the border at which, say, rights become privileges, laws become tyranny, comedy becomes cruelty, empathy becomes naivete, quirkiness becomes an annoyance, protests become violence, etc. are equally as complex. The more we consider and analyze (zoom in on) these borders of concepts, the more we may realize that where one becomes the other is ultimately arbitrary. Sure, such cut-off points of definitions may be thought of as objective, but objective to whom? An individual’s personal experience is largely out of one’s control, and the interpretations of such experiences are generally, if not solely, mediated by previous sets of experiences. If what makes my cut-off point different than another’s is simply a matter of where I was born or how I was raised or by certain events that have occurred in my life versus others, what makes mine more correct than anyone else’s other than the fact that they are mine?

Yes, all numbers do indeed land on one side of the Mandelbrot Set border or the other. All numbers are either inside of the Mandelbrot Set or outside of it. But there’s nothing determining which is which other than what that particular number is. The fact is that two numbers that are tremendously close to each other can behave dramatically differently when under these iterations. Just the slightest change in what number is chosen can have a huge impact on what happens to it, when iteratively sent through the equation. Where these behaviors differ is along the border. Though perfectly mathematical, the border is largely unpredictable, just like conceptual borders are ultimately dependent on unpredictable individuals.

The Mandelbrot Set is also a fractal, a term coined by Benoit Mandelbrot himself in the 1970’s. The idea of a repeating pattern of self-similarity is a hallmark of fractal geometry. One of the better known “basic” fractal shapes is called the Sierpinski Triangle:

Sierpinski Triangle, credit: https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle

As you can see, there are triangles inside triangles inside triangles, etc. One can imagine zooming into this image forever, but also zooming out forever. The pattern would repeat in the exact same way, infinitely.

But the Sierpinski Triangle doesn’t involve the use of the so-called imaginary number, so there’s no complexity to the pattern - it’s all perfectly predictable. Zooming in on the Mandelbrot Set border, however, reveals patterns of similar traits, including mini-Mandelbrot shapes and mini-bulbs, but not in a perfectly predictably repetitive way. One would likely tire quickly of watching a zoom-in video of a Sierpinski Triangle, while Mandelbrot zoom-in videos remain interesting for much longer. Indeed, billions of hours of such videos have been watched online.

This is all because of the complexity that comes in part from the usage of i, the so-called imaginary number, defined as the square root of -1. Yes, the idea of a number that, times itself, equals a negative number, is beyond conception, but the mathematical rules that follow remain logical. Adding this imaginary aspect to the iterated equation is what gives the Mandelbrot Set its unique patterns of self-similarity, where all the shapes look familiar, sometimes exactly like others, but within a new context. What we see in a Mandelbrot Set border zoom-in could be considered a “random pattern,” and it’s actually rather mesmerizing. But you never quite know exactly what’s coming next. The shapes that seem to make the border are shown to be made of other similar shapes, which are then shown to be made of others, and so on. The self similarity, like the border itself, is infinite.

Pictured is the needle of the Mandelbrot Set, where there lies a “mini-brot", a smaller version of the entire shape. These mini-brots appear infinitely throughout the set, as one zooms in on the border. https://www.rgbstock.com/photo/nzieWw2/Fractal+Needle

The concept of what a fractal is began to be recognized everywhere. The branches of a tree are self similar versions of the tree itself, each offshoot a smaller similar version of its parent. A plant’s roots are obvious fractals as well. Lightning branches into a fractal pattern across the sky during a storm. The human vascular system is fractalized, among many other bodily systems and organs that can be thought of fractally. From the largest veins, to the smallest capillaries, the average human vascular system, if stretched out end to end, would wrap itself more than twice around the Earth. In nature, fractals are exploited for efficiency.

Everything from clouds to leaves to cellular tissues to lungs to crystals are all fractals. It was a fractal-shaped antenna design that ultimately allowed for modern cell phone reception as we know it (link). The animation industry integrating fractal qualities into their software was the main factor for the development of dramatically more realistic graphics, starting in the late 2000s (link). The universe itself is a fractal pattern of planets that revolve around stars that revolve around black holes along with hundreds of billions of other stars in a galaxy among trillions of galaxies, imagined further by some as merely one “bubble” or one version in an infinite world of universes, including an infinite number of universes just like our own. For, what is the multiverse if not the fractal of all fractals?

Fractal-like pattern contained within the structure of a leaf. Credit: https://www.reddit.com/r/pics/comments/bya9sn/fractal_leaf_vein_patterns_looks_like_a/#lightbox

The structure of families is fractal, as children and offspring of all creatures are self-similar versions of their parents. As such, DNA can be thought of as the code to ensure this, itself a fractal pattern of molecules (link). Even growth rates of populations are governed by patterns modeled by a real version of Mandelbrot-like iterations (link). It was the discovery of fractals and everything that came along with them that led to the wider branch of mathematics known as chaos theory, the word chaos a slight misnomer, as there’s always an underlying mathematical scheme, but the outcomes are not easily predicted nor easily mathematically modeled.

As we zoom into the Mandelbrot Set border, the pattern we see is unpredictable, non-repeating, and infinite. But there is indeed a pattern. It makes sense. It’s a combination of randomness and determinacy. Like a timeless song, or a subtly hilarious meme, though humanly created, it’s as if the notes or the joke could never have been any other way. Once witnessed, the pattern’s acceptance is inevitable.

Partly predictable and partly indeterminate is roughly our experience of the passage of time. We can imagine the next instant with a generally helpful degree of accuracy. But which sight, sound, smell, feeling, event, or decision suddenly or eventually jars you off what feels like your intended track and distracts you from your wrongly envisioned future is largely unpredictable. We know whatever happens will happen for reasons, but those reasons are currently unknown.

Perhaps this is why so many humans find something like a Mandelbrot Set zoom-in video so mesmerizing; it’s a rough simulation of the passage of time and the human experience itself. Regardless, “being among fractal patterns” has been shown to have a calming effect on humans. Nature provides fractals everywhere. The aforementioned trees, plants and clouds are among the immediately obvious examples. And all of these fractals are filtered, perceived and interpreted, at least in part, by the most complex system known to man - a fractal itself - the human brain.

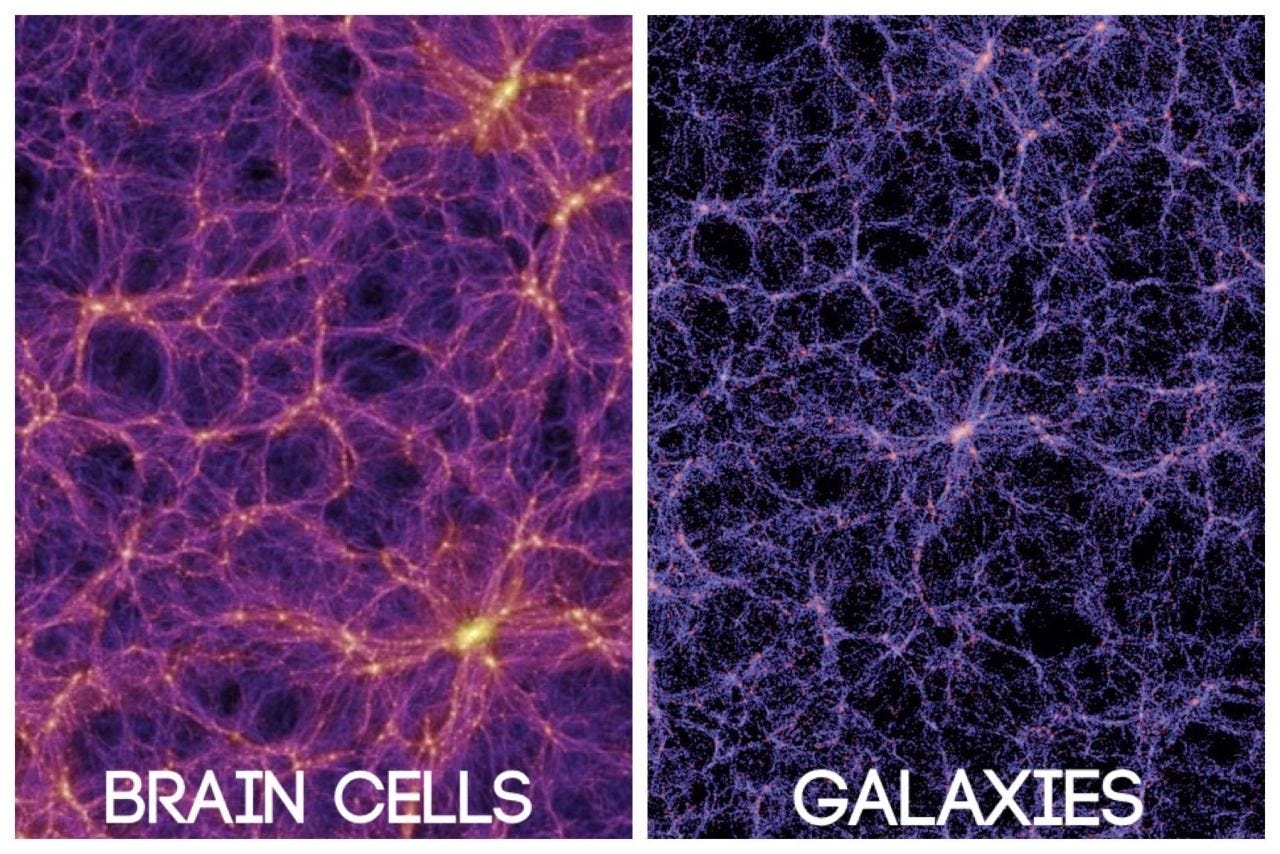
There are about 100 billion neurons within the average adult human brain. There are, at the low end of the approximation, 100 billion stars in our galaxy, so in a strange sense, humans may indeed be “galaxy-brained”. But in terms of a visual comparison, the more recent apparent similarity comes from an image of a neural network adjacent to that of the vast cosmos.

Image credit https://foglets.com/the-universe-as-like-human-brain-discover-scientists/

Are human brains a smaller version of the universe itself? If so, how are they connected? Are our brains like the fractal antenna that receives the information from the universe at large? It makes some sense for one to be a self-similar version of the other. If so, is the universe a brain of sorts? Are all the galaxies connected somehow? This could help explain the mystery of so-called dark matter which is what is thought to be needed to account for, among other things, keeping outer stars of galaxies from flying off into space. Dark matter also seems necessary to hold galaxy clusters together. But, to be clear, what’s really happening is Einstein’s equations stop working in these particular scenarios. While most physicists generally assume that there must be more “stuff” out there, gravitationally holding things together that we simply cannot see, it’s entirely possible that there isn’t more stuff at all, but rather unseen connections from within a broader context.

Zooming in on the Mandelbrot set reveals an endless supply of Mandelbrot shapes within Mandelbrot shapes; patterns within patterns. If the universe is indeed a fractal, something like the galaxies and neural networks being similar things is no longer surprising. We know self-similarity at scale occurs naturally in math and mathematically in nature. Supposing, then, a broad connection between what is being understood and the mechanism largely responsible for this understanding isn’t exactly controversial. There being a connection at all requires a faith that everyone has. The type of connection that exists becomes a matter of personal preference, but the base level of “magic” is always acknowledged either implicitly or otherwise. An understandable universe is only surprising when one assumes otherwise.

Physicist Eugene Wigner wrote about “the unreasonable effectiveness of math in the Natural Sciences” in a 1960 article of the same title. But, what level of mathematical effectiveness would be reasonable? A so-called theory of everything would be unreasonable, but to model parts of the physical universe with extreme precision using formally defined mathematical structures can only be considered but so special. Not having sufficient natural language to account for physical behavior doesn’t help, but without an imminent need for ontological explanations, the math suffices just fine. This, among other things, can lead people to believe in math itself being some base-level truth or an ultimate reality of its own. This is known as Platonism. But this, like all other attempts at broad encapsulations, doesn’t completely work.

We are not the Mandelbrot Set. We are not numbers. Neither math nor physics nor logic, nor philosophy nor art nor any combination thereof will ever, in any formulation, account for the entirety of anything, much less everything. Each has their relevance and importance. Each creates and is created by context. Each can and does point to the greater ultimate truth of existence that can be experienced, felt and truly known on the deepest of levels, but never fully, formally and foundationally defined or spoken. To make a Chirstian analogy, our brains are as much a fractal of the universe as Mary was the mother of God. Stories are told in many forms. Infinity is expressed in many languages.

More than a somewhat abstract brain-to-universe fractal idea, however, the physical brain itself - the brain matter - is indeed a fractal shape, a system once again efficiently fitting itself into a compact area by being able to fold in on itself. The most complex system known to man, the human brain, is also one of the largest organs of the human body. Beyond that, the map of neurons that reside within the brain create an overall branch-like fractal design, and within this structure, fractal communication takes place as signals branch across a system of neurons similar to lightning we might see spread across the night sky during a storm.

More recently, it’s been shown that fractal neuronal communication takes place during “phase transitions” of the brain (link). Which phases these correlate to is still unknown, but these fractal firings occur in humans, mice, and even fruit flies. So, self similarity across size scale occurs within the neuronal firings themselves and when comparing brains at large.

Information processing, learning, remembering, making decisions: these are all things we give the brain credit for. But from afar, brains participate in a feedback loop of information exchange. The fractal flickerings of light that take place in our brains seem to translate, at least roughly, to parts of our mental experiences. Many assume that these flashes, and whatever is responsible for them, in some way, explains the totality of our conscious experience. To those of this mindset, believing anything else would be akin to believing in magic. However, it’s just as easily argued that it is the materialists themselves that indeed accept the magic of an unexplained “conscious emergence” from otherwise unconscious matter. Assuming that this magic can, in principle, be explained physically is therefore immediately self-defeating. But anyone arguing in favor of what “everything is fundamentally,” whether matter, consciousness, God, energy, information, computation, spirit, love, space, or time, will always be wrong.

As physicist Carlo Rovelli stresses, each interpretation of quantum mechanics has its usefulness, and therefore none is necessarily right or wrong. This is ultimately the result of the limit of conceptual thought, as we’ll only be able to define any given concept through other concepts. Rovelli, a thinking man’s physicist, has further linked his relational interpretation of physics to the Buddhist idea of sunyata, translated as emptiness. Rovelli found a connection of what we find in physics to Buddhist principles, specifically that of ancient buddhist philosopher Nagarjuna. With all things being relational, there can be no “autonomous essence.” Searching for the absolute within an inevitably relative framework eventually leads one to this emptiness.

But before we celebrate that “everything is nothingness,” we must remind ourselves that doing so finds ourselves guilty of what we just argued against. The fact that there is no conceptually definable base layer of reality doesn’t then mean that emptiness or nothingness is now that base layer. This gives emptiness absolute status in the name of not being able to give anything absolute status - a paradoxical contradiction. The key is to understand that it’s not that everything is emptiness, but rather that “everything is emptiness,” the difference being that the latter statement admits to a contextual requirement. We can understand the statement’s intent when prefaced properly, but on its own, it’s rather trite and meaningless. Indeed, on the surface, stating that “everything is empty” can easily be viewed as immediately contradictory, if not meaningless.

This is similar to what we see with computer scientist and philosopher Bernardo Kastrup’s criticism of the Buddhist connection that Rovelli has made to what he believes we see in physics. Kastrup takes issue with Rovelli’s sudden change from objective discovery to a subjective reality. Much of Kastrup’s criticism seems to stem from the contradiction of making an objective statement about subjectivity. Kastrup wants to make the relational nature of existence a fact of the absolute.

From Kastrup’s Blog:

“Rovelli takes a purely objective path to the conclusion that the physical world is entirely relational. He uses explicit, conceptually clear logical reasoning and empirical evidence to do so. He goes where this reasoning and evidence take him, all the way until a point where the inevitable implication is something he doesn't seem to like: that there must be a deeper, non-physical and non-relational layer to reality, which grounds the relationships that constitute the physical world, giving semantic meaning to the very word 'relationship.' From that point on, Rovelli arbitrarily abandons all post-Enlightenment epistemic values and switches to a vague, ambiguous, hand-waving, second-hand appeal to the mystical insights of someone who is no longer around to clarify what he meant. Never mind that the result is a peculiar Frankenstein monster, neither objective nor subjective; that Rovelli managed to avoid a conclusion he doesn't like—he describes how relieved he was upon reading Nāgārjuna, because the latter freed him from the pressure of having to find out what the underlying essence of reality is—seems satisfactory to him.”

Source: https://www.bernardokastrup.com/2021/06/here-i-part-ways-with-rovelli.html

But, whether or not there is an underlying essence of reality is unknowable if we accept the necessarily relational aspect of conceptual thought, physical measurements and informational transfer, as Rovelli has. The ultimate, absolute, foundational nature of reality then, by definition, is indeed unknowable in the conceptual sense. But either direction you go from there will be a contradiction. Stating that “the base layer of reality is relational” is itself an absolute statement and therefore self-contradictory; as is the statement that “there is no base-layer of reality.” Again, it’s a self-contradiction.

But this is not a problem with Rovelli’s or Nagarjuna’s philosophies. It’s the problem of our necessarily limited conceptual thought processes invoked to create and understand contexts from within the natural world when applied to the world at large. Disagreements are inevitable. Practically no philosopher agrees in totality with another about such things, and many continue to argue in semantic and logical circles as has been done for centuries. Believing in expressible absolutes leads us all down paths of contradiction, dissatisfaction, and even unrest, anger and fear.

Yes, from any given perspective, we may find that the world can seem tautological, arbitrary, incomplete, inconsistent, contradictory, relative, subjective, random, empty, infinite, infinitely regressive, infinitely dualistic, logically circular, self-referential, paradoxical or singular - often a certain combination thereof, depending on the context. But the world is not those things. These are simply the inevitable landing spots when we attempt to know the world in totality, an inherently impossible task. As such, it’s truly unsurprising that practically all criticisms of others’ philosophies involve accusations of the above-listed concepts. But again, these criticisms stem from an underlying and generally unspoken, though always problematic assumption that absolutes not only exist, but that they can be expressed fully. Even though Kastrup acknowledges the pitfalls of attempts at verbalizing the inconceivable, he still takes great issue with Rovelli’s connection of attributes of the physical world to a central tenet of Buddhism. Predictably, he describes Rovelli's take as self-contradictory, arbitrary, and infinitely regressive.

Philosophers and people in general often feel compelled to cling to these false absolutes in an effort to avoid the seemingly meaningless conclusions we find. Dogmatic religious zealots and blindly loyal political or social ideologues find themselves in this category. Militant atheistic thought, however, is equally as problematic, as it embraces the false absolute of provability.

How to live one's life, then, becomes simply a matter of attempting to take each context on its own merits, understanding that each perspective is worthy in its own right. “The middle way” is the Buddhist phrase that attempts to encapsulate this type of understanding. Being an atheist within one context, and a believer within another seems impossible because within all these concepts and their definitions resides the concept of “you,” or the “I” of the self. Realizing that, just like all other relative concepts, there is no “I” as such, is the true differentiator among levels of understanding.

From Rovelli’s “Helgoland”:

“And myself, looking at the star, do I exist? No, not even I. So who is observing the star? No one, says Nagarjuna. To see a star is a component of that set of interactions that I normally call my ‘self’. ‘What articulates language does not exist. The circle of thoughts does not exist.’ There is no ultimate or mysterious essence to understand that is the true essence of our being. ‘I’ is nothing other than the vast and interconnected set of phenomena that constitute it, each one dependent on something else. Centuries of Western speculation on the subject, and on the nature of consciousness, vanish like morning mist.”

Found in the Mandelbrot Set are a tremendous amount of mathematical surprises. For example, one can calculate approximations of pi with just a little Mandelbrot mathematical reverse engineering. The Golden Ratio, through the Fibonacci numbers representing the number of tendrils each bulb has as one “zooms in” along the main Mandelbrot carotid boundary, is also present, much more evidently so. The simplest way to imagine growth is to take two things, then add the difference. It’s a way of taking two things and making a third thing by adding the difference of the things to the new bigger thing. It only requires two things and knowledge of what makes them different. The Golden Ratio is the easiest way of this relationship, and thus the most natural. Certain things do indeed grow in this way, as we see the Golden Ratio throughout nature.

Does nature somehow “know” about the Golden Ratio, or is this just our human way of making sense of randomness? Does the Golden Ratio create fractals or is it the other way around? What’s more fundamental: the numbers, equations and mathematical concepts that Benoit Mandebrot used to discover the famous shape with an infinitely complex and self-similar border, or the Mandelbrot Set itself? While it’s fun to watch Mandelbrot zoom-in videos online and bask in the beauty and wonder of the random patterns that seem to encompass so much of our physical and mental existence, it’s important to understand that in trying to answer such questions, the fact that there can be no complete and conceptually satisfying explanation is itself the most beautiful truth of all.